독립변수가 두개 이상인 경우, Partial Differential Equations

Laplacian Operator

From Taylor expansion,

re-express as,

Relaxation Method in 2-Dimensional Space

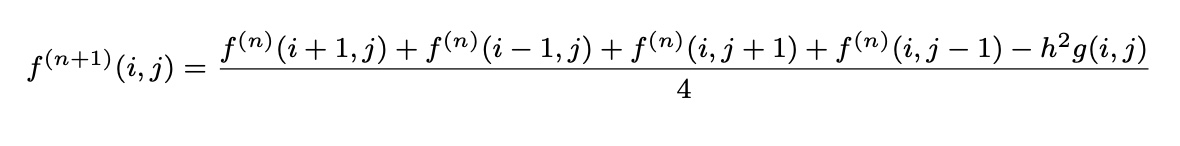
ex)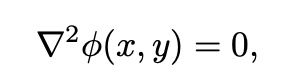

B.C; V=1 and grid spacing h=1cm and L=1m

import numpy as np

import matplotlib.pyplot as plt

M=100

V=[0, 1.]

tolarence=1.e-3

phi=np.zeros([M+1, M+1], float)

phi[0, :]=V[1]

phitmp=np.zeros_like(phi, float)

phitmp[0, :]=V[1]

delta=1.

while delta>tolarence:

for i in range(1, M):

for j in range(1, M):

phitmp[i][j]=(phi[i+1][j]+phi[i-1][j]+phi[i, j-1]+phi[i, j+1])/4

delta=np.max(abs(phi-phitmp))

phi, phitmp=phitmp, phi

plt.imshow(phi)

# plt.gray()

plt.show()

Poisson Equation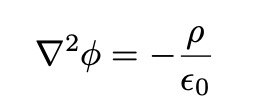

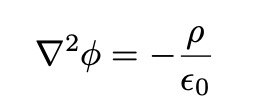
ex)

import numpy as np

import matplotlib.pyplot as plt

M=100

V=[0, 1.]

tolarence=1.e-6

h=0.01

phi=np.zeros([M+1, M+1], float)

phitmp=np.zeros_like(phi, float)

rho=np.zeros([M+1, M+1], float)

# coordi left up (0, 0)

for i in range(60, 80):

for j in range(20, 40):

rho[i, j]=1.

rho[j, i]=-1.